Nul besoin de savoir résoudre les équations de Maxwell, mais un minimum de théorie me semble utile afin d'éviter les grossières erreurs et les déceptions. Vous trouverez ici une synthèse des régles physiques qui sous-tendent le fonctionnement des antennes cadre utilisées pour la réception VLF.
Cette page présente successivement la théorie des antennes cadre, à air ou ferrite, l'étude des divers élements constitutifs du schéma équivalent électrique et propose une modélisation sous SPICE.
La section Références propose à ceux souhaitant approfondir ces notions une liste de sources d'informations.
Pour ceux qui sont totalement allergiques aux équations, une synthèse à la fin de chaque chapitre résume les concepts abordés et les principales conclusions.
Un peu de théorie
Principe de fonctionnement d'une antenne cadre
Le rôle de toute antenne de réception est de convertir une onde électromagnétique en tension. Une antenne cadre magnétique est un enroulement de fil de cuivre autour d'un cadre (cadre à air) ou autour de ferrites (cadre ferrite).
En réalité, une antenne cadre est sensible au champ magnétique et non au champ électrique (d'où son nom de cadre magnétique). La loi de Faraday exprime que pour un cadre constitué d'un conducteur électrique et soumis à un flux magnétique variable Φ(t) une force électromotrice e(t) apparaîtra a ses bornes (circuit ouvert) )selon la relation :
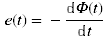 (1)
(1)où :
- e(t) est la force électromotrice, en V
- Φ est le flux magnétique traversant le circuit, en webers (Wb ≡ V·s)
Cette équation est valide pour des antennes électriquement courtes par rapport à la longueur d'onde de l'onde électromagnétique en question, ce qui est le cas pour les fréquences qui nous intéressent.
On définit alors :
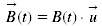 est le vecteur du champ d'induction magnétique, u vecteur unitaire
est le vecteur du champ d'induction magnétique, u vecteur unitaire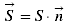 est le vecteur normal à la surface du cadre, n vecteur unitaire
est le vecteur normal à la surface du cadre, n vecteur unitaire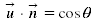 où θ est l'angle orienté
où θ est l'angle orienté 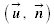 entre les lignes du champ et la normale au cadre.
entre les lignes du champ et la normale au cadre.
Le flux magnétique représente la quantité de lignes de force du champ d'induction magnétique passant à travers le cadre :
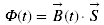 (2)
(2)
Pour un champ magnétique sinusoïdal, uniforme sur la surface S, l'amplitude B(t) projetée selon n est :
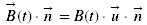 (3)
(3)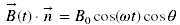 (4)
(4)où :
- B0 est l'intensité du champ d'induction magnétique, en tesla (T ≡ Wb/m² ≡ V·s/ m²)
- ω est pulsation du champ d'induction magnétique, en rad·s-1
L'équation (2) devient alors :
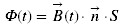 (5)
(5)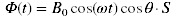 (6)
(6)
Pour un cadre de N spires, chacune de surface A, on a
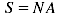 , d'où :
, d'où :
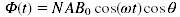 (7)
(7)et (1) devient :
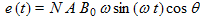 (8)
(8)
Sachant que 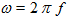 , la valeur efficace de la tension induite à la sortie de l'antenne s'exprime en fonction champ d'induction magnétique :
, la valeur efficace de la tension induite à la sortie de l'antenne s'exprime en fonction champ d'induction magnétique :
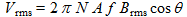 (9)
(9)Expression de la tension induite en fonction du champ électrique
L'efficacité d'une antenne est mesurée au travers de la notion de hauteur effective he selon la relation:
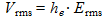 (10)
(10)où :
- Vrms est la valeur efficace de la tension induite à la sortie de l'antenne, en V
- he est la hauteur effective, en m
- Erms est la valeur efficace du champ électrique au niveau de l'antenne, exprimée en V/m
Sachant que 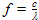 et que le champ électrique est en relation avec le champ magnétique d'induction selon la formule
et que le champ électrique est en relation avec le champ magnétique d'induction selon la formule 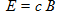 , la hauteur effective d'une antenne cadre est :
, la hauteur effective d'une antenne cadre est :
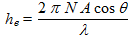 (11)
(11)où :
- he est la hauteur effective, en m
- N est le nombre de tours du bobinage
- A est la surface de chaque enroulement, en m²
- λ est la longueur d'onde, en m
- θ est l'angle entre les lignes du champ et la normale au cadre
Avec une cadre ferrite, le champ électromagnétique d'induction dans l'antenne est multiplié par la perméabilité magnétique relative du matériau. L'équation (9) devient alors :
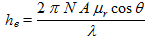 (11 bis)
(11 bis)où :
- µr est la perméabilité magnétique relative, sans dimension. µr dépend du matériau.
Un petit calcul montrera que, compte tenu des longueurs d'ondes considérées (15km à une fréquence de 20kHz), la hauteur effective d'une antenne cadre sera forcément ridicule devant la longueur d'onde... Mais tout n'est pas perdu, et il est néanmoins possible d'obtenir de bons résultats avec des moyens raisonnables.
Expression de la tension induite en fonction du champ magnétique
Le champ d'induction magnétique traversant le cadre est fonction de la composante magnétique de l'onde électromagnétique (appelé H ou champ d'excitation magnétique) et de la perméabilité magnétique du milieu.
Le champ d'induction magnétique B est en relation avec le champ d'excitation magnétique H selon :
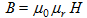 (12)
(12)où :
- B est la valeur efficace du champ d'induction magnétique, en tesla (T ≡ V·s/m²)
- µ0 est la perméabilité magnétique du vide, constante universelle valant 4π10-7 H/m.
- µr est la perméabilité magnétique relative, sans dimension. µr dépend du matériau.
- H est la valeur efficace du champ d'excitation magnétique, en A/m
Pour un cadre à air, on a µr = 1.
Pour un cadre ferrite, les lignes de champs sont concentrées par les propriétés ferromagnétiques du milieu, et µr peut atteindre des valeurs de quelques centaines à quelques milliers.
L'antenne fournira donc une tension efficace Vrms pour une valeur efficace du champ d'excitation magnétique Hrms selon la relation :
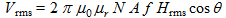 (13)
(13)
Synthèse
Le rôle de toute antenne de réception est de convertir une onde électromagnétique en tension. Une antenne cadre magnétique est un enroulement de fil de cuivre autour d'un cadre (cadre à air) ou autour de ferrites (cadre ferrite).
Une antenne cadre est sensible au champ magnétique et non au champ électrique (d'où son nom de cadre magnétique). Elle fournit une tension proportionnelle à ce champ. Une particularité de ce type d'antennes est de fournir une tension proportionnelle à la fréquence.
Les paramètres influant sur la sensibilité de l'antenne sont le nombre de tours du bobinage, la section de chaque spire. Dans le cas d'une antenne ferrite, la perméabilité du matériau permet d'accroitre la tension aux bornes.
D'autre part, ce type d'antenne a deux lobes dont l'amplitude est maximale dans le plan du cadre et nulle (en théorie) dans le plan perpendiculaire au cadre.
Schéma équivalent électrique
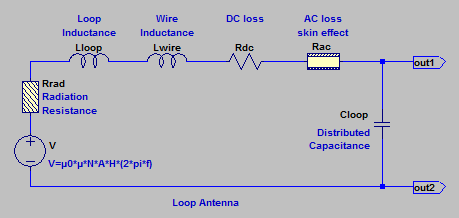
Le schéma électrique équivalent d'une antenne cadre est constitué:
- d'un générateur de tension idéal V dont la tension est dépendante du champ d'excitation électrique selon l'équation (13)
- de la résistance de rayonnement Rrad
- de l'inductance du cadre Lloop
- de l'inductance du fil Lwire
- de la résistance du fil Rdc
- de la résistance due à l'effet de peau et à l'effet de proximité Rac
- de la capacité distribuée Cloop
Paramètres du modèle
Les éléments résistifs, inductifs et capacitifs sont des éléments "perturbateurs" qui influencent chacun l'efficacité de l'antenne. Nous allons maintenant analyser leur contributions respectives.
Les équations présentées ci-dessous sont, sauf mention contraire, applicables aux cadres à air et aux antennes ferrite. Pour les cadres à air, on a µr=1. Pour une antenne ferrite, µr dépend du type de ferrite, de ses dimensions et de la longueur du bobinage.
Résistance de rayonnement Rrad
La résistance de rayonnement traduit les "pertes" dans l'antenne lors de la transformation de l'énergie électromagnétique en énergie électrique. A la différence d'une résistance ohmique qui transforme l'énergie électrique en chaleur, cette résistance est virtuelle, et à ce titre, elle n'est pas souce de bruit thermique selon la formule de Johnson-Nyquist. Sa valeur est :
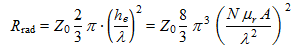 (14)
(14)où :
- Rrad est la résistance de rayonnement, en Ω.
- Z0 est impédance caractéristique du vide, en Ω.
- µr est la perméabilité magnétique relative, sans dimension. µr dépend du matériau.
- N est le nombre de tours du bobinage
- A est la surface de chaque enroulement, en m².
- λ est la longueur d'onde, en m.
Sachant que 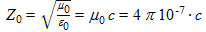 l'équation (14) devient :
l'équation (14) devient :
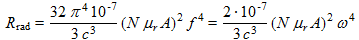 (15)
(15)Inductance du cadre Lloop
Antenne cadre à air
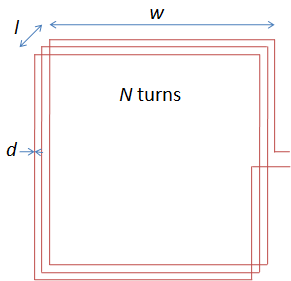
L'enroulement du fil autour d'un cadre a une inductance qui peut être calculée pour un cadre carré selon la formule :
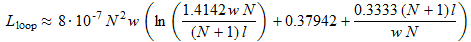 (16)
(16)où :
- Lloop est la l'inductance du bobinage, en H
- N est le nombre de tours du bobinage
- w est la largeur du cadre, en m
- l est la longueur du cadre, en m
Antenne Ferrite
L'enroulement du fil autour de la ferrite a une inductance qui peut être calculée par :
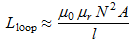 (16 bis)
(16 bis)where:
- Lloop est la l'inductance du bobinage, en H
- µ0 est la perméabilité magnétique du vide, constante universelle valant 4π10-7 H/m.
- µr est la perméabilité magnétique relative, sans dimension. µr dépend du matériau.
- N est le nombre de tours du bobinage
- A est la surface de chaque enroulement, en m²
- l est la longueur du cadre, en m
Inductance du fil Lwire
Le fil utilisé pour le bobinage présente lui-même une inductance. Un fil de longueur 4
Nw présente une inductance
Lwire selon :
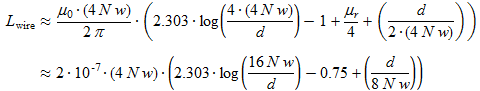 (17)
(17)où :
- Lwire est la l'inductance du fil, en H.
- N est le nombre de tours du bobinage.
- w est la largeur du cadre, en m. La longueur totale du fil est 4Nw.
- d est le diamètre du fil, en m.
Résistance du fil Rdc
Le fil électrique présente une résistance dépendant de sa longueur et de son diamètre. La résistance d'un fil de longueur 4
Nw et de diamètre
d est calculée selon l'équation :
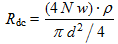 (18)
(18)où :
- Rdc est la résistance du fil, en Ω.
- N est le nombre de tours du bobinage.
- w est la largeur du cadre, en m. La longueur totale du fil est 4Nw.
- d est le diamètre du fil, en m. La section du fil est πd²/4.
- ρ est la résistivité du cuivre, en Ω·m. ρ=16.78nΩ·m.
Cette résistance est une source de bruit blanc thermique selon la formule de Johnson-Nyquist qui exprime la densité spectrale en tension du bruit selon : 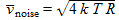 , en V/Hz½.
, en V/Hz½.
k est la constante de Boltzmann (1.38·10-23 J/K), T est la température absolue en kelvins, et R est la valeur de la résistance en ohms.
Résistance due à l'effet de peau et à l'effet de proximité Rac
A la résistance en courant continu identifiée ci-dessous se rajoute une résistance en haute fréquence du fait que le courant électrique n'a plus une répartition homogène. Notamment, l'effet de peau traduit le fait que le courant a tendance à se déplacer uniquement sur les bords du conducteur. L'effet de proximité est la perturbation de la répartition de courant par la présence de conducteurs proches.
Bien que son effet puisse être supérieur à celui de l'effet de peau, l'effet de proximité est extrêmement délicat à modéliser car entièrement dépendant de la géométrie de l'enroulement. Il sera donc ignoré ici.
La résistance due à l'effet de peau est par contre modélisée par l'équation :
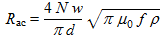 (19)
(19)où :
- Rac est la résistance due à l'effet de peau, en Ω.
- N est le nombre de tours du bobinage.
- w est la largeur du cadre, en m. La longueur totale du fil est 4Nw.
- d est le diamètre du fil, en m. Le périmètre du fil est πd.
- µ0 est la perméabilité magnétique du vide, constante universelle valant 4π10-7 H/m.
- f est la fréquence, en Hz.
- ρ est la résistivité du cuivre, en Ω·m. ρ=16.78nΩ·m.
Capacité distribuée Cloop
La capacité distribuée est répartie tout au long du bobinage. Sa valeur approximative pour un cadre carré est donnée par :
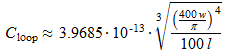 (20)
(20)où :
- Cloop est la capacité distribuée d'un cadre carré, en F
- w est la largeur du cadre, en m
- l est la longueur du cadre, en m
Cette formule est aussi applicable aux antennes ferrite en remplaçant w par le diamètre des enroulements.
Exemple pratique
Afin de mieux cerner les contributions respectives des divers paramètres du schéma équivalent, voici les valeurs calculées dans un cas concret classique. Considérons un cadre carré de
w=60 cm de côté, avec
N=50 tours de fil de cuivre émaillé #26 (diamètre
d=0.405mm) bobinés sur une longueur
l=1cm.
Les paramètres du modèle sont alors :
- Rrad=12.5pΩ à 10kHz, 0.125µΩ à 100kHz et 1.25mΩ à 1MHz...
Compte-tenu des fréquences qui nous intéressent, ce paramètre peut être négligé.
- Lloop=5.77mH
- Lwire=318µH
- Rdc=15.6Ω
- Rac=2.43Ω à 10kHz, 7.67Ω à 100kHz et 24.3Ω à 1MHz.
On peut constater que l'effet de peau est non négligeable par rapport à Rdc. D'autre part, ce calcul ne prend pas en compte l'effet de proximité, qui est probablement beaucoup plus important que l'effet de peau, compte tenu du bobinage serré de notre antenne.
- Cloop=129pF
Synthèse
Le schéma électrique équivalent d'une antenne cadre est constitué :
- d'un générateur de tension idéal dont la tension est dépendante du champ d'excitation électromagnétique
- d'une inductance, constituée principalement de l'inductance du cadre et dans une moindre mesure de l'inductance du fil de cuivre
Divers paramètres viennent perturber le fonctionnement de l'antenne :
- une résistance de rayonnement qui traduit les "pertes" dans l'antenne lors de la transformation de l'énergie électromagnétique en énergie électrique. Cette résistance peut être généralement négligée.
- la résistance du fil de cuivre, à laquelle s'ajoute aux hautes fréquences une résistance due à l'effet de peau et à l'effet de proximité. Les effets de peau et de proximité sont largement dépendant de la géométrie de l'antenne et ont généralement un ordre de grandeur équivalent ou supérieur à la résistance en courant continu du fil.
- une capacité parasite, distribuée entre tous les enroulements de l'antenne. Elle peut être négligée en première approximation.
Modélisation SPICE d'une antenne cadre
Description du modèle SPICE
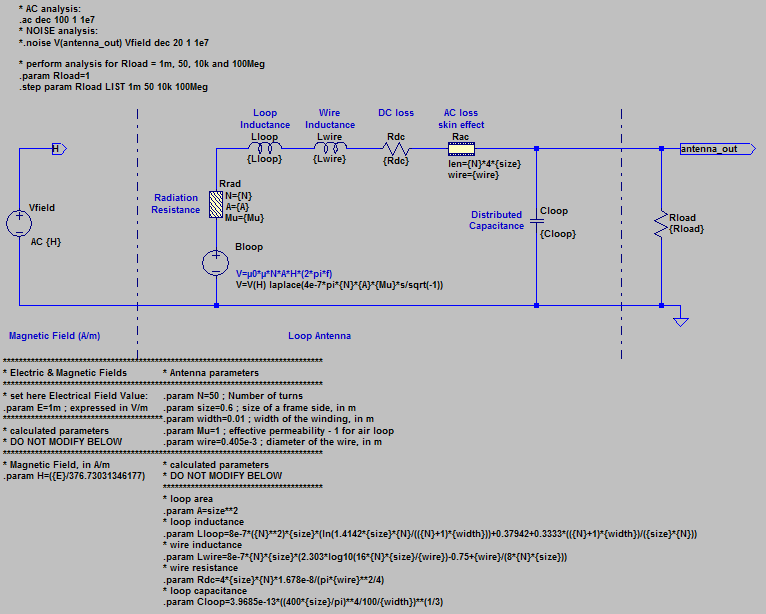
La copie d'écran ci-dessous décrit le modèle SPICE de l'antenne cadre.
Le générateur de tension idéal Bloop implémente la formule (13). Une transformée de Laplace est utilisée pour traduire la dépendance à la fréquence. Vfield est un générateur de tension simulant un champ électromagnétique de 1mV/m.
Le reste du schéma implémente les divers élements du schéma équivalent électrique de l'antenne et les diverses équations permettant de déterminer leurs valeurs.
Enfin, l'antenne est reliée à une charge purement résistive Rload. Les simulations sont faites avec des charges de 1mΩ (circuit fermé), 50Ω (impédance classique d'un récepteur), 10kΩ (impédance d'une carte son) et 100MΩ (circuit ouvert).
Utilisation de l'antenne en tension
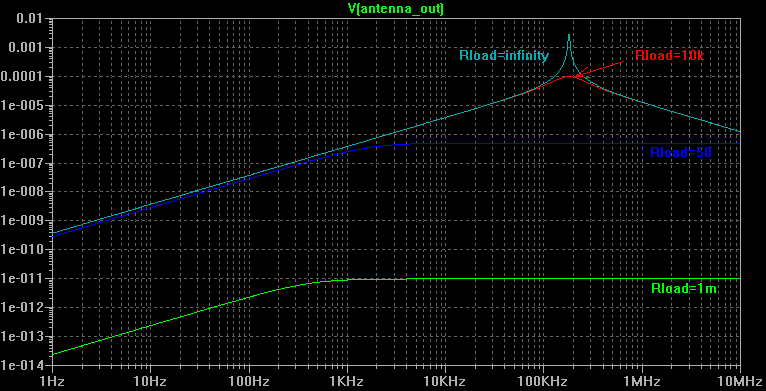
La simulation fournit les résultats suivants pour la tension aux bornes de l'antenne :
Si l'on s'intéresse à la courbe en circuit ouvert, on constate une réponse linéaire avec une pente de 20dB/décade correspondant à l'évolution selon la fréquence de Bloop.
A partir d'environ 100kHz, le circuit devient résonnant. La fréquence de résonance obéit à l'équation (a) ci-dessous :
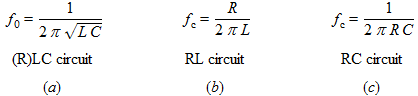 (21)
(21)
Ici, L=Lloop+Lwire=6.09mH, et C=Cloop=129pF, ce qui donne f0=180kHz.
Au-delà, l'impédance de la capacité distribuée Cloop devient suffisamment faible pour limiter la tension de sortie.
En rajoutant une charge résistive, la résonance est atténuée et la courbe de réponse s'aplanit au détriment du niveau de sortie. D'autre part, deux pôles sont créés :
- un filtre passe-haut créé par (Lloop+Lwire) et (Rload+Rdc+Rac).
- un filtre passe-bas entre Cloop et Rload.
Avec
Rload=50Ω, en utilisant les équations (21 b) et (21 c), on obtient un passe haut avec une fréquence de coupure à environ 1.8kHz et un passe-bas avec une fréquence de coupure à environ 25MHz.
Accord de l'antenne
L'ajout d'une capacité Ctune aux bornes de l'antenne permet de l'accorder sur une fréquence particulière. En utilisant l'équation (19 a) nous pouvons calculer la capacité à utiliser.
Supposons que nous souhaitions accorder notre antenne sur NAA, 24kHz. Connaissant l'inductance (Lloop+Lwire=6.09mH), nous obtenons Ctune+Cloop=7.22nF, soit Ctune=7.09nF.
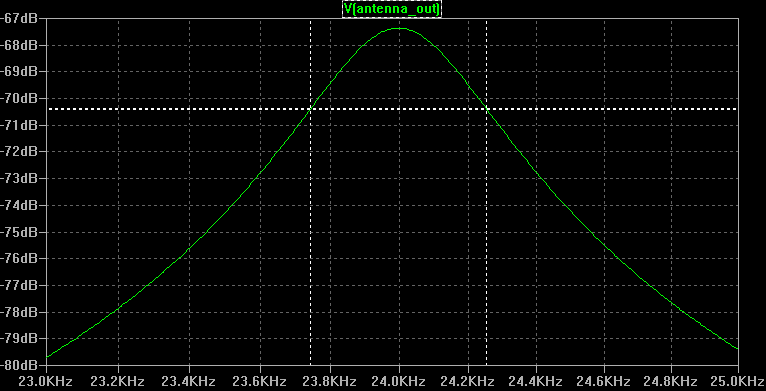
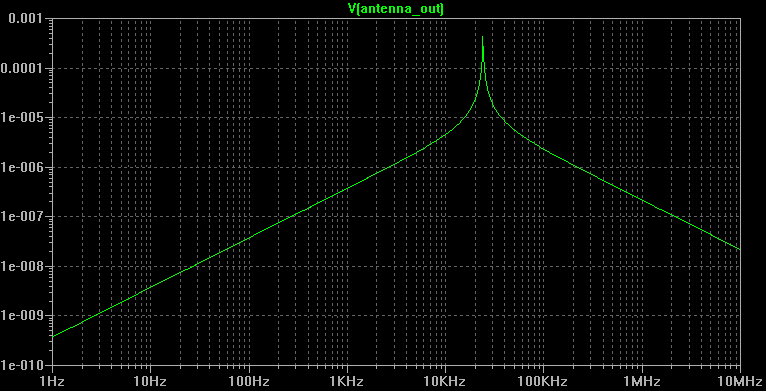
La réponse en fréquence de l'antenne est alors :
L'équation (20) permet de calculer le facteur de qualité de l'antenne :
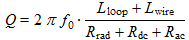 (22)
(22)Dans notre cas particulier, nous avons Rac=3.76Ω à 24kHz, ce qui donne Q=47.4.
Nous pouvons mesurer ce facteur de qualité en mesurant la bande passante Δf à -3dB et grâce à la formule :
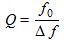 (23)
(23)
La bande passante mesurée est d'environ 509Hz, ce qui donne un Q mesuré de 47.2, en accord avec le calcul théorique.
Une station à proximité (par exemple DHO38 sur 23.4kHz) sera atténuée (d'environ 8dB dans ce cas).
En pratique, le facteur de qualité de l'antenne réelle sera plus faible du fait de l'effet de proximité qui n'est pas pris en compte dans cette simulation.
Utilisation de l'antenne en courant
La simulation fournit les résultats suivants pour le courant dans la charge de l'antenne :
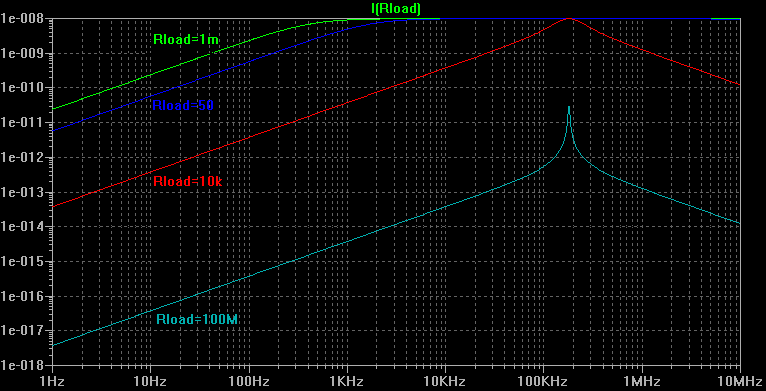
Si l'on reboucle l'antenne sur un circuit fermé, la réponse en fréquence est plate. La perturbation due à la capacité distribuée est supprimée car celle-ci est court-circuitée.
A basses fréquences, l'antenne est vue comme une résistance. A hautes fréquences, cette résistance devient négligeable devant l'impédance due à l'inductance du cadre. Cette impédance (jLω) est proportionnelle à la fréquence. Le générateur de tension étant lui-aussi proportionnel à la fréquence—cf. équation (13)—, le courant devient constant en fonction de la fréquence.
La transition entre le domaine résistif (basses fréquences) et le domaine inductif (hautes fréquences), se fait selon l'équation (19 b). La valeur obtenue pour cette fréquence de coupure est légèrement supérieure à 400Hz dans notre cas.
Un amplificateur opérationnel monté en convertisseur courant-tension permettra d'offrir une charge presque nulle à l'antenne. Pour ce cas particulier, l'utilisation d'une transrésistance de 100kΩ permettra d'avoir une réponse linéaire de 1V/V·m-1 sur l'ensemble de la bande VLF et au-delà.
L'utilisation d'une charge non nulle réduit la plage de linéarité de l'antenne, jusqu'à retrouver le comportement résonnant étudié plus haut dans le cas du fonctionnement en tension de l'antenne.
Synthèse
La modélisation SPICE permet d'établir deux cas optimaux d'utilisation d'une antenne cadre :
- si l'on est intéressé par une seule fréquence, il est possible d'accorder l'antenne par un condensateur placé à ses bornes. L'antenne doit alors être utilisée à haute impédance afin de maximiser le facteur de qualité de l'antenne.
- si l'on désire travailler en large bande, il faut faire travailler en courant en la court-circuitant, par exemple par l'intermédiaire d'un amplificateur opérationnel monté en convertisseur courant-tension. La bande passante n'est limitée aux fréquences basses que par la résistance intrinsèque de l'antenne.
Références
Vous trouverez de précieuses informations dans les ouvrages de référence suivants (malheureusement en anglais) :
| • The ARRL Antenna Book |  |
| • The ARRL Handbook for Radio Communications |  |
| • Le site www.vlf.it est une excellente source d'explications et de cas pratiques de constructions d'antennes. |  |
| • The Art of Electronics. Horowitz and Hill. La référence de l'électronique! |  |
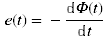 (1)
(1)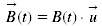 est le vecteur du champ d'induction magnétique, u vecteur unitaire
est le vecteur du champ d'induction magnétique, u vecteur unitaire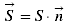 est le vecteur normal à la surface du cadre, n vecteur unitaire
est le vecteur normal à la surface du cadre, n vecteur unitaire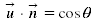 où θ est l'angle orienté
où θ est l'angle orienté 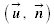 entre les lignes du champ et la normale au cadre.
entre les lignes du champ et la normale au cadre.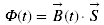 (2)
(2)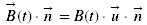 (3)
(3)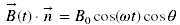 (4)
(4)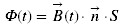 (5)
(5)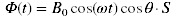 (6)
(6)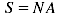 , d'où :
, d'où :
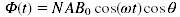 (7)
(7)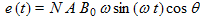 (8)
(8)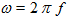 , la valeur efficace de la tension induite à la sortie de l'antenne s'exprime en fonction champ d'induction magnétique :
, la valeur efficace de la tension induite à la sortie de l'antenne s'exprime en fonction champ d'induction magnétique :
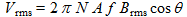 (9)
(9)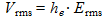 (10)
(10)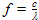 et que le champ électrique est en relation avec le champ magnétique d'induction selon la formule
et que le champ électrique est en relation avec le champ magnétique d'induction selon la formule 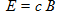 , la hauteur effective d'une antenne cadre est :
, la hauteur effective d'une antenne cadre est :
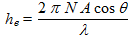 (11)
(11)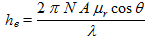 (11 bis)
(11 bis)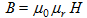 (12)
(12)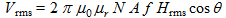 (13)
(13)
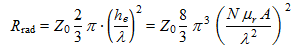 (14)
(14)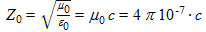 l'équation (14) devient :
l'équation (14) devient :
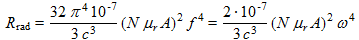 (15)
(15)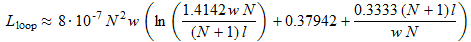 (16)
(16)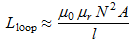 (16 bis)
(16 bis)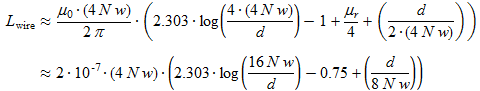 (17)
(17)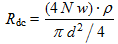 (18)
(18)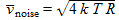 , en V/Hz½.
, en V/Hz½.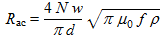 (19)
(19)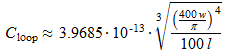 (20)
(20)
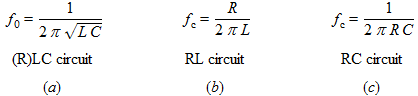 (21)
(21)
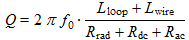 (22)
(22)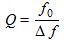 (23)
(23)