The basic questions when building an antenna are which size and how many turns. As usual, "the bigger, the better" is a mis-conception and the Laws of Nature are not that simple.
As explained in the antenna theory page, bigger antennas and more turns means increased signal level at the output of the antenna. But this also means increased noise.
This page should help you in finding the optimal antenna characteristics for your application.

Firstly, it contains an analysis of the antenna noise, with a characterization of its influence with respect to the natural or man-made radio noise expected at VLF.
Then, the section Signal-to-Noise ratio is a synthesis of calculation of SNR for various antenna sizes and frequencies of interest.

Antenna Noise

Two noise sources influence the output of the antenna:

• the radio noise, whether natural or man-made.
• the noise of the antenna itself.

We have no influence on the radio noise, we can just install the antenna in a place as quiet as possible, that is away from EMI sources. But we can try and minimize the noise of the antenna and its preamplifier in order to reduce it to levels lower than the radio noise. The radio noise is described in the P.372 recommendation of the ITU. It is modelled in the radio noise page.

Antenna noise sources

The resistances are the main antenna noise sources. Each resistance is a source of white thermal noise. The power spectral density of this noise does not depend of the frequency.
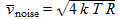The noise generated by a resistance is: (Johnson-Nyquist formula).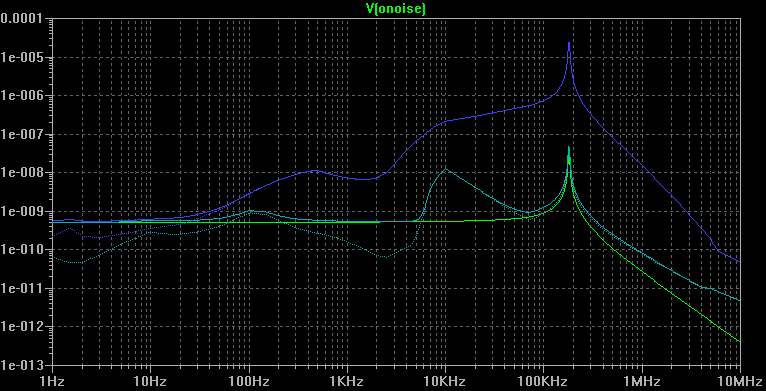
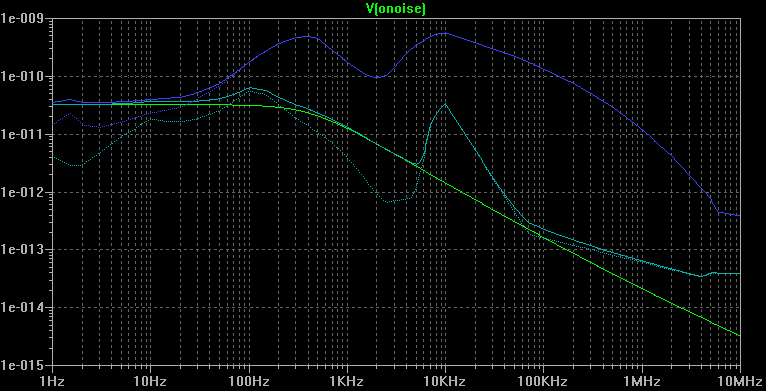
v_noise is the noise voltage spectral density, in V/Hz^½, k is the Boltzmann constant (1.38·10^-23 J/K), T is the absolute temperature in kelvins, and R is the resistance value in Ω.
By using copper wire with an important cross section, it is possible to reduce the wire resistance as well as the high frequency resistance.

Antenna noise voltage (high impedance) and current (low impedance)

SPICE gives the following results for the voltage noise when the antenna is connected to high impedance receiver:
SPICE gives the following results for the voltage current when the antenna is connected to low impedance receiver:

The current plots show the current noise spectral density, in A/Hz^½. Those values are obtained by adding at the output of the antenna an ideal operational amplifier acting as a current-to-voltage converter with a noiseless transresistance of 1Ω. The noise voltage spectral density calculated by SPICE at the output of the converter reflect the current noise spectral density at the shorted outputs of the antenna.

The green line corresponds to the noise of the antenna only.

The blue solid line corresponds to the sum of the maximum expected radio noise and of the antenna noise.
The blue dotted line corresponds to the maximum expected radio noise only.

The cyan solid line corresponds to the sum of the minimum expected radio noise and of the antenna noise.
The cyan dotted line corresponds to the minimum expected radio noise only.

We see that, in both voltage and current analysis, the noise contribution of the antenna gets preponderant on the radio noise only below about 70Hz for maximum radio noise conditions, and below about 6kHz for ideal radio noise conditions.

Here are the figures obtained in various configurations:

	Frequency range	Antenna only	Antenna + Min Radio Noise	Antenna + Max Radio Noise
RMS Voltage	1Hz-10MHz	2.75µV	4.64µV	2.37mV
	10kHz-100kHz	205nV	878nV	150µV
RMS Current	1Hz-10MHz	833pA	2.39nA	97.0nA
	10kHz-100kHz	140pA	1.62nA	77.6nA

In this case, the antenna noise is not significant for VLF waves reception. This would not be the case for the reception of ULF, SLF or ELF waves.

Antenna Signal-to-Noise Ratio

The antenna dimensions have to be sufficient to generate signal levels high enough with respect to the sensibility of the receiver.
Under those circumstances, the most important parameter to take into account is the signal-to-noise ratio. The higher, the more easily useful faint signals can be extracted from the background noise.
This section contains the SNR values determined by SPICE simulations of square loop antennas of various sizes and number of turns. The model used here corresponds to a non-tuned antenna working in current.

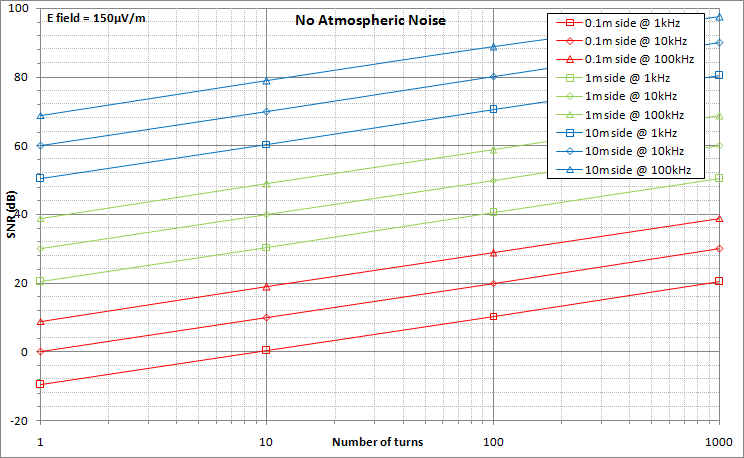
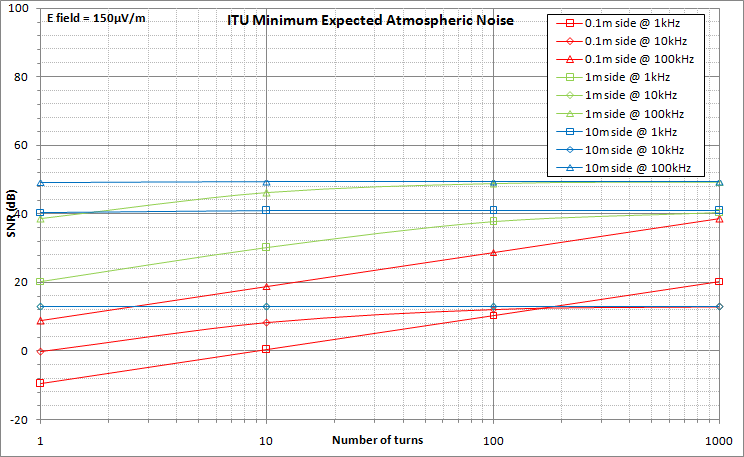
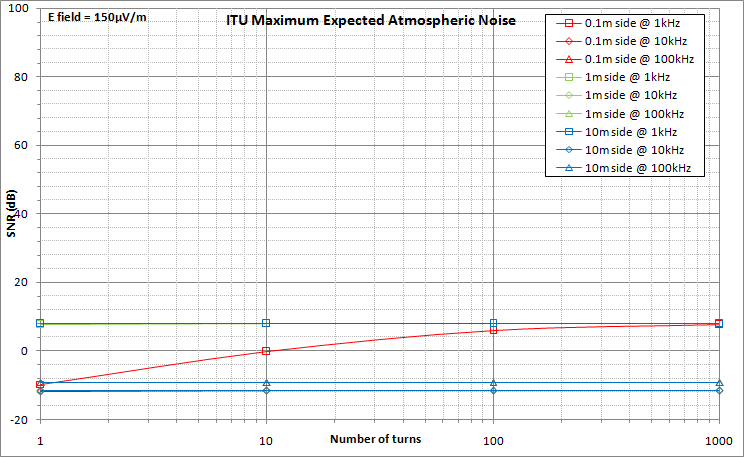
The three graphs here below show the SNR values (vertical axis, in dB) against the number of turns (horizontal axis).
Plots for antenna sizes of 0.1m by 0.1m (4" by 4"), 1m by 1m (3.3ft by 3.3ft) and 10m by 10m (33ft by 33ft) are shown.
For each antenna size, the SNR values have been determined around the frequencies of 1 kHz, 10 kHz and 100 kHz. Those three frequencies are in the linearity range of the antenna working in current. To ensure consistency, the following bandwiths have been used for the noise calculations:

• 10 Hz around 1 kHz
• 100 Hz around 10 kHz
• 1 kHz around 100 kHz

The calculations have been made for a electric field of 150 µV/m at the antenna, which is a reasonnably moderate signal level.

The first graph assumes that there is no radio noise. This is a theoretical and ideal situation, where the noise figure is only influenced by the antenna noise. In this case, one can clearly see the influence of the antenna dimensions on the SNR ratio:

• a tenfold increase in the antenna size corresponds to a gain of 30dB on the SNR. Basically, the signal increases by 40dB (signal voltage is proportional to the antenna area, and so to the square of the size) and the noise increases by 10dB (thermal noise voltage is proportional to the square root of the wire resistance, and so to the square root of the wire length).
• a tenfold increase in the number of turns corresponds to a gain of 10dB on the SNR. Basically, the signal increases by 20dB (signal voltage is proportional to the wire length) and the noise increases by 10dB (thermal noise voltage is proportional to the square root of the wire resistance, and so to the square root of the wire length).

The second graph corresponds to actual conditions where the radio noise is minimal. To reach those noise levels, the best possible location must be chosen (away from man-made noises) and atmospheric noise must be low.
Even under those excellent circumstances, one can see that the antenna efficiency with respect to SNR gets non linear with respect to size or number or turns. For a "big" antenna (10m side), the number of turns has no effect at all, so a single turn antenna is sufficient, for all frequencies of interest. For an antenna with a side of 1m, the influence of the number of turns gets marginal above a few tens of turns.

The last graph corresponds to worst case conditions of radio noise. In this case, the influence of the antenna characteristics on its overall capability to extract useful signal from the overwhelming noise is quite limited.